Continuity is when you can make a graph without taking your pencil off the paper. It is when the graph has no breaks, no jumps, no holes, no oscillating behavior (basically a bridge). The graph is predictable, meaning that the graph goes where you would assume it would go. The limit of the function (discussed later) and the value of the function are the same number. The graph is a smooth, not rigid. The key thing to remember is that just because it changes functions, does not mean that it is not continuous still.
 (http://www.inf.kcl.ac.uk/research/groups/PLANNING/index.php?option=com_content&view=article&id=70&Itemid=77)
(http://www.inf.kcl.ac.uk/research/groups/PLANNING/index.php?option=com_content&view=article&id=70&Itemid=77)In the picture above, the graph has a lot of odd changes in shape, but it is still a continuous graph. No matter what x value you choose, the limit and the value will be the same number, there are no breaks in the graph, and it can be drawn without taking the pencil off of the paper.
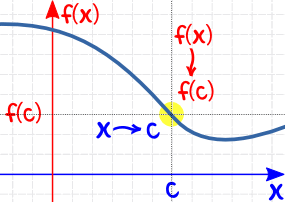
(http://www.mathsisfun.com/calculus/continuity.html)
This is also a continuous graph. The values of f(x) (limit) is the same as that of f(c) (value). This is a more a graph that more people are able to associate with more easily. Both this and the previous graph are continuous graphs though. Continuities are seen on a lot of graphs. It is a continual graph, no breaks, predictable, and has the same limit and value.
A discontinuity is what we see as a break, jump, or hole in the graph. These are the graphs that are fragmented and broken. They do not run in a smooth line. They stop abruptly at some points and continue again at either the same x value in a different spot or at another part on the graph. We have two different families of discontinuities. The first family is known as a removable discontinuity. They are removable for specific reasons (discussed in part 3). The only removable discontinuity that we have is known as a point discontinuity.This looks like a hole in the graph.

(http://www.tutorvista.com/content/math/discontinuity/)
This is a point discontinuity because it creates a hole in your graph. It has a limit, but it does not have a defined value. The value is undefined because there is something in the function that prevents the graph from reaching that point on the graph. The limit is where that hole is though because it was the spot that the graph intended to reach.

(http://hardycalculus.com/calcindex/IE_discontinuity.htm)
This is also a point discontinuity because it has the break in the graph. However, unlike the one that we looked at above, this one has a value (the darker red dot). The limit is the spot on the graph where the hole exists (the intended height of that x value in that spot) and the value is the red dot because that is the actual value of the function at that x-value. Both are examples of removable discontinuities (can mathematically make the function work).
There are also other discontinuities that are known as non-removable discontinuities because they cannot be changed. There are three types of discontinuities: jump, infinite, and oscillating behavior.
The first is a jump discontinuity. The graph breaks at one point and either continues below or above that spot in the same x position. The graph can either have to open circles or one open and one closed. An open circle means that the graph cannot touch that value and a closed circle means the graph touches that value (hence why we cannot have two open circles). The limit does not exist here because the graph has two different values for the same x value (different left/right values). The graph looks like this:

(http://en.wikibooks.org/wiki/Calculus/Continuity)
As you can tell, the value of 0 has a left value of -1 and a right value of 1, creating a jump in the graph and therefore making it a discontinuity. The limit does not exist, but the value does.
Another discontinuity is the infinite discontinuity. It gets its name because as it heads to a certain point on the graph, it turns towards either infinite of negative infinite and creates a vertical asymptote in the graph ( a spot where the graph will head to that point, but never actually touch it). This creates unbounded behavior on the graph making a break in the graph, denying the value of x to have a limit or a value, and making it a discontinuous graph. It looks like this:

(http://shell.cas.usf.edu/~ssuen/2233.2013s/c/chapter1.diagrams/images01.html)
The graph is discontinuous because it has the infinite discontinuity at -3 creating the vertical asymptote and unbounded behavior.
The third and final discontinuity is known as oscillating behavior. This is when in a very small portion of the graph, it creates a large amount of closely knit wiggly lines. It is a discontinuity because the graph is never intending to go to a certain point for that x-value. It is just wiggly. It creates an untraceable line and does not have a limit or a value. It cannot be fixed.
(http://en.wikipedia.org/wiki/Classification_of_discontinuities)
This an example of oscillating behavior because prior to the point on the graph where it hits zero on the y-axis, the graph just wiggles. It creates so many up and down portions that they blur together and make it look like a solid mass on the graph. It does not intend to go anywhere and it contains no value.
In the end, continuity is when the graph has no breaks, no jumps, no holes, is predictable, has the same number for the limit and value, and can be drawn without taking your pencil off of the paper. A discontinuity is a break, a jump, a hole, a non-matching limit and value, not predictable, and cannot be drawn without taking the pencil off of the paper.
2. Limit or Value?
A limit is the intended height of a graph, the point that it meant to go to, but might not have actually "reached". The limit only exists for removable discontinuities and for continuous graphs. This is because the graph actually reaches a point on the graph. The jump, infinite, and oscillating behavior discontinuities do not have a limit because they never touch an intended point or they have two y-values for a single x-value that will never connect with one another, or because it just wiggles too much in too small of an area. The limit is reached only for a point discontinuity because if you trace the graph from both sides to that point, you get to a single point. With all the other points, no single point is reached meaning there was no intended height and there was no limit.
(http://math.stackexchange.com/questions/137609/proving-the-non-existence-of-a-limit)
This is an example of when the limit does not exist. The left and right limit statements come to two different values and the graph does not meet at a single intended height meaning that the limit does not exist. However, the value does exist. The values is the filled in circle and that is at 1. See the difference there?
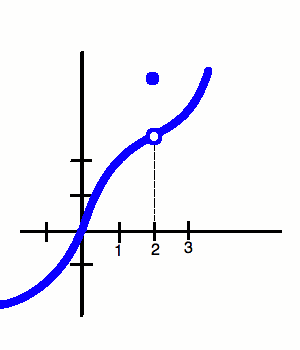
(http://www.wyzant.com/resources/lessons/math/calculus/limits)
Here the limit and the value both exist. The limit exists because the graph touches in the same spot (the left and right limit statements are the same). The graph meets at 3 when the x-value is 2. That is the limit, the intended height. The actual value is the darker circle which seems to be visible at 5. This is an example when both exist. For a continuous graph the limit and the value will be the same for the whole entire graph.
3. A.N.G.
Do not fear. This is not some kind of gang. This is the three letters from the word VANG that we use for limits: Algebraically Numerically and Graphically.
Algebraically is when we use either direct substitution, factoring out/dividing method, rationalizing/conjugate method, or limit infinity. The video below has some spots where it is blurry, but the examples are there for the first three methods to help you get the basic understanding of each type. Remember you always want to use direct substitution first!
(https://www.youtube.com/watch?v=8z4aofW85K4)
This next video explains how to algebraically solve one dealing with infinity. Do not fear it is simpler than it seems. The video explains things a little bit differently than learned in class, but the idea and the shortcut are there.
(https://www.youtube.com/watch?v=75xO9xy7TTQ)
Numerically: This is when we use a table to find the values of the function as you get closer and closer to the
number. It helps you find what the limit should be and then when you solve for it you see if the limit actually exists. You should usually take the number being approached and add and subtract 1/10 and move closer in two on either side. In the video he uses 1/100. As long as you are getting extremely close to the number it is okay.
Graphically: This is when you take your fingers, trace the graph to the point you want to get to and see what the limit is. From there you can see if the limit is present or if it does not exist. If it does not exist, you write one sided limit statements to help you understand where each part (the left and the right) pieces of the graphs are going. It is not too difficult and is pretty simple to understand.
(https://www.youtube.com/watch?v=IEfoQeWm8Fc)
Resources
http://www.inf.kcl.ac.uk/research/groups/PLANNING/index.php?option=com_content&view=article&id=70&Itemid=77
http://www.mathsisfun.com/calculus/continuity.html
http://www.tutorvista.com/content/math/discontinuity/
http://hardycalculus.com/calcindex/IE_discontinuity.htm
http://en.wikibooks.org/wiki/Calculus/Continuity
http://shell.cas.usf.edu/~ssuen/2233.2013s/c/chapter1.diagrams/images01.html
http://en.wikipedia.org/wiki/Classification_of_discontinuities
http://math.stackexchange.com/questions/137609/proving-the-non-existence-of-a-limit
http://www.wyzant.com/resources/lessons/math/calculus/limits
https://www.youtube.com/watch?v=75xO9xy7TTQ
https://www.youtube.com/watch?v=8z4aofW85K4
https://www.youtube.com/watch?v=IEfoQeWm8Fc