I/D#1: Unit N Concept 7: The Unit Circle and how it relates to Special Right Triangles.

Inquiry Activity Summary

 

1) 30 Degree Right Triangle

 

Here we have the 30 degree triangle. In the picture above we see the steps to labeling and finding the vertices of a special right triangle known as the 30-60-90 right triangle. The first thing to do is to label it according to the rules of special right triangles. This step is done in purple. It is the labeling of the vertical side, horizontal side, and the hypotenuse with the right values. The hypotenuse is labeled as 2x, the horizontal values is x radical 3, and the vertical value is simply x. The next thing that you need to do is make the hypotenuse equal to the value of one. To do this you need to divide each side by the value of the hypotenuse (2x). This step is done in green. When you divide each value by 2x your new values become 1 for the hypotenuse, radical 3 over 2 for your horizontal value, and you get 1/2 for your vertical value. After you have the new values you can label the triangle with the variables r,x, and y. When you do this you label the hypotenuse r, the horizontal side x, and the vertical value y. You then create a small chart with the new variable and the previously found value to make sure everything is clear. That step is done in red. Then you draw a graph so that the triangle is located in the first quadrant. Make the 30 degree angle the vertex with an ordered pair of (0,0). The 90 degree angle will be the horizontal value, zero-(radical 3/2, 0) and the point at the 60 degree mark as the horizontal value, vertical value- (radical 3/2, 1/2). This last value is the first mark on the unit circle.

2) 45 Degree Right Triangle

This is also a special right triangle. This one is known as the 45-45-90 triangle. The steps to solving this one are the same as the last, but the numbers are different than the last one. The first step is to label the sides according the rules of a special right triangle. The hypotenuse is to be labeled x radical 2. The vertical side is to be labeled x and so is the horizontal side. After that you want to reduce the hypotenuse to be equal to one. To do so divide every side by the value of the hypotenuse (x radical 2). The new values are shown in green. You get the hypotenuse to be 1, the vertical and horizontal sides (because they had the same value) become radical 2/2. This is done because when you divide by a radical you must rationalize it because radicals do not belong in the denominator. To do this you multiply it by radical 2 over radical 2. After that you label the sides with the variables of r,,x, and y. Label the hypotenuse r, the horizontal side x, and the vertical side y. After you do that create a small table matching the variable and the new value together. This is shown in red in the photo above. The r is equal to 1, the x any y are equal to radical 2/ 2. The next thing you do is to draw a graph so that you place the triangle in the first quadrant. Make the bottom 45 degree angle the origin with an ordered pair of (0,0). Then you move to the 90 degrees and label it as the horizontal value and zero (that is the distance that you have moved). The ordered pair is (radical 2/2, 0).  The top 45 degree angle has an ordered pair of the horizontal value and the vertical value, making it (radical 2/2, radical 2/2). That is all that is to it, This last ordered pair then becomes the second set of pairs on the unit circle. Very important to understand.

 

3) 60 Degree Right Triangle

This is our final special right triangle. It had the same values as the first special right triangle, but in different locations. It is known as the 60-30-90 right triangle. Label your hypotenuse 2x, your vertical side x radical 3 (this value always goes with the 30 degree angle) and your horizontal side as x (this value always follows the 60 degree angle. Compare this one with the 30-60-90 and see how they remain with the angle measures not sides). Then you have to make the hypotenuse equal 1 so divide each side of the triangle by 2x. When you do this you get three new values for each side. Your hypotenuse is 1, your horizontal side is 1/2, and the vertical side is now radical 3/2. This is shown in green in the picture. Then you label the sides with the variables of r,x, and y. The hypotenuse is r, the vertical side is y and the horizontal side is x. Then you match the values with the new variables. To do this create a chart with the variables and the new values. This is done in red in the picture. It is r equals 1, x equals 1/2, and y equals radical 3/2. After that is done you draw a graph so that the triangle sits in the first quadrant. Then you must label the vertices. The origin (0,0) should be at the bottom 45 degree angle. Then move down the line to the 90 degree angle and label that one x value,0 (1/2, 0). Finally go to the 30 degree angle at the top and label it the x value, y value (1/2, radical 3/2). This last ordered pair becomes your third value on the unit circle. It is very important to see this.

 

4) Derivation of the Unit Circle Assistance

(http://www.mathsisfun.com/geometry/unit-circle.html)

This activity helps you derive the unit circle because these three triangles are used for the whole circle. The top ordered pair for each triangle can be seen in each quadrant once. The values remain the same except the signs will change depending on the quadrant. From this picture though you can see how the ordered pairs keep on reappearing in the circle. The triangles make the circle a reality. The triangles in each quadrant are found the same way as the first quadrant. This works because as you move in the revolution of the circle, the larger degrees have the reference angles of the special right triangles. This is seen in the photo above. The triangles are the same in each quadrant. Below is a video that shows this happening. The person doing this is showing how no matter where you are in the circle you will have these right triangles seen. When you see that reference angle that has that 30 degrees or that 45 degrees or the 60 degrees you can follow the rules and know the ordered pair for that angle. The second video goes into details describing how the patterns are seen and where they are located in each quadrant. Both producers of the videos are showing that the right triangles are located in each quadrant just sitting in different positions.


(http://jwilson.coe.uga.edu/EMT668/EMAT6680.2001/Bruce/instructunit/day_3.htm)

(http://en.wikiversity.org/wiki/Polar_Coordinates)



 

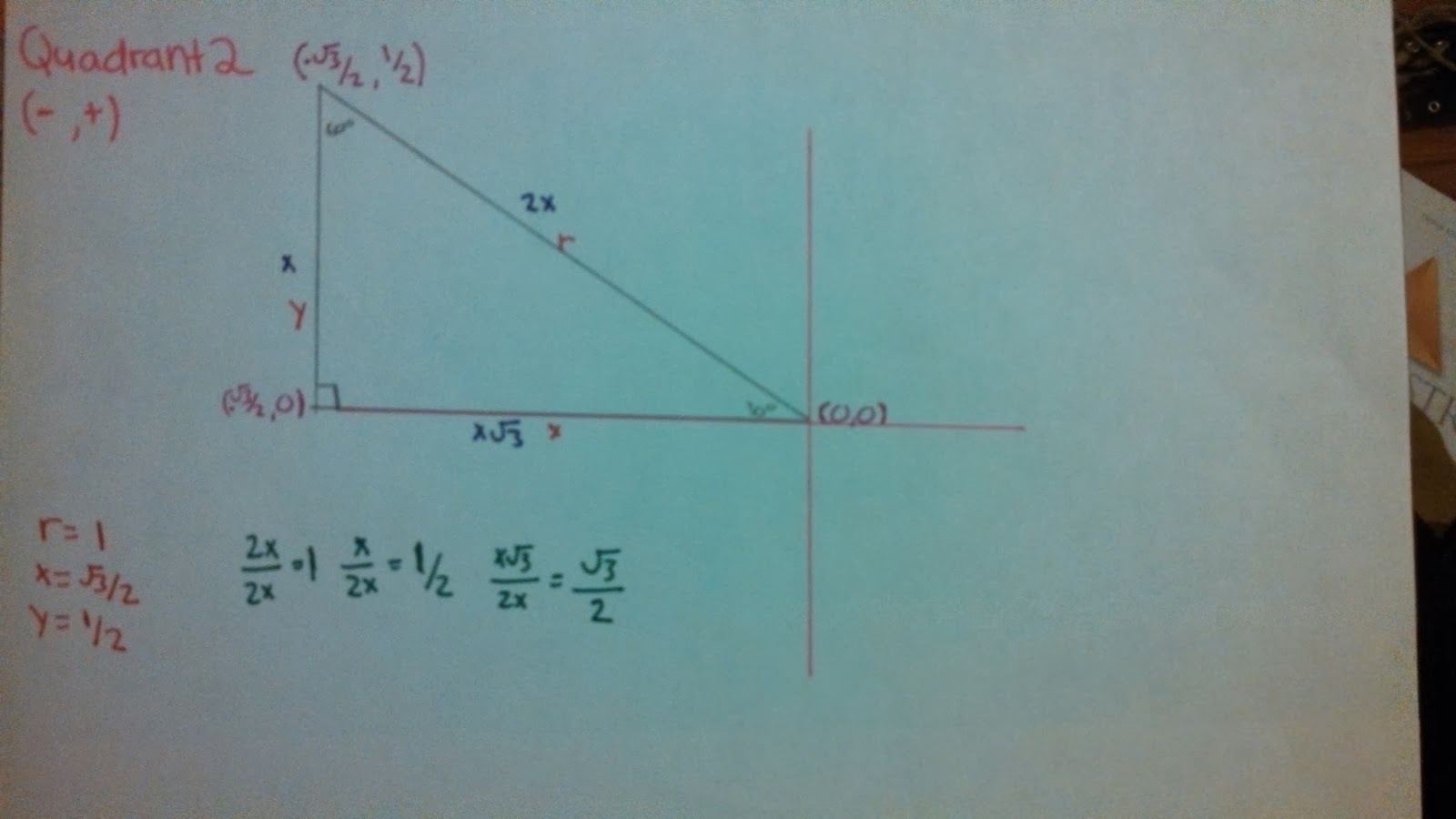
5) Other Quadrants 

 

In the different quadrants the only thing about the triangles that change are that the ordered pairs will contain one or two negative values. That is due to the location of the triangle though. We know that in quadrant one they are both positive. In quadrant two the x value is negative and the y value is positive. In the third quadrant both the values are negative and in the fourth quadrant. Those are the only things that are different in the other quadrants. Nothing else changes. If you look at the images above and compare them to the quadrant one pictures you will notice that each one is identical in the process of finding it and the only thing that changes is the sign of the ordered pair. The reason that happens is it is adjusting to the different quadrant locations. Nothing else is happening to them.

(http://catalog.flatworldknowledge.com/bookhub/reader/128?e=fwk-redden-ch03_s01)

Inquiry Activity Reflection

The coolest thing I learned from this activity was that the right triangles work in all the different quadrants and that the relationship is there. I slowly realized it last year, but I was more focused on simply passing the exam last year to really appreciate it. It Is actually a very interesting thing to understand and get to use. It was very cool to learn.

This activity will help me in this unit because it will allow me to understand and easily place the ordered pairs for the triangles in the different quadrants. By doing this activity I can figure out where the triangles are in the different quadrants if I forget the pattern. This activity has allowed me to have the tools to derive the circle if I need to in a given situation.

Something I never realized before about special right triangles and the unit circle is that they were all interlocking. They work for all of the quadrants and not just the first one. I knew they worked in the first one for sure, but seeing how they worked in the other quadrants was really interesting to see. I did not fully realize that until after completing the activity. It is important to deriving the unit circle and 3 days ago I learned that. Thank you Special Right Triangles!
Resources
http://www.mathsisfun.com/geometry/unit-circle.html

http://catalog.flatworldknowledge.com/bookhub/reader/128?e=fwk-redden-ch03_s01
http://jwilson.coe.uga.edu/EMT668/EMAT6680.2001/Bruce/instructunit/day_3.htm
http://en.wikiversity.org/wiki/Polar_Coordinates



RWA#1: Unit M Concepts 4-6: Conic Sections in Real Life

1. An ellipse is the set of all points such that the sum of the distance from two points is a constant.  (http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/ellipse-drawn-from-definition-geogebra-dynamic-worksheet)
2.

(http://www.tpub.com/math2/Job%202_files/image777.jpg)



Standard Form

An ellipse has two standard forms. If you look at the image above you can see that the first one has a^2 under the x. This indicates that the graph will be a fat graph and that your major axis is equal to y and the minor axis will be equal to x. This is because the graph will have a constant y while the x changes to make the graph extend horizontally. The second equation has the a^2 under the y. This means that your graph will be skinny and that your major axis will be equal to x and your minor axis will be equal to y. This is due to the fact that your x will remain constant as you move up and down, stretching it vertically.

Center

The ellipse has a center just like every other conic. The center will always derive from the x and y binomials. If you look at the picture above, you see that x is paired with an h and y is paired with a k. Those are the numbers that you will use to write your center. The center is opposite of the numbers represented in the binomials. That means that if h is positive in the parenthesis then it will be negative in the ordered pair and vice versa. It is an easy concept to understand and you want to make sure that you do not forget to switch the signs. Remember that h will always be your x coordinate and k will always be your y coordinate.

A and B

When you look at the image above you see a^2 and b^2. These denominators will help you determine what your vertices and co-vertices will be and also help you determine your c and foci. The square root of the larger denominator will be your a. The a is the distance between your center and each of your vertices. The whole major axis is a distance of 2a. (vertex to vertex). This will allow you to figure out what your vertices are. You will move a spaces up and down or left and right depending on your graphs shape. The b is similar. You will find b by taking the square root of the smaller denominator. The b is the distance from your center to each of your co-vertices. That is either up and down or left and right from the center depending on the graphs shape. The length of the minor axis is put in terms of 2b (co-vertex to co-vertex). The b will also let you indicate what your co-vertices are by counting from the center on the minor axis that many spaces. Besides this though is the fact that they allow you to find your c.

C

The c is an important part of the graph. The c allows you to figure out your eccentricity and your foci. Your c is found by taking a^2 and subtracting b^2 to get c^2. Then you take the square root of c and simplify if possible. That answer will become your c. The c is then later used to find your foci and eccentricity.  The equation is also shown below.

 

(http://www.mathwarehouse.com/ellipse/images/formul-focus.gif)

Foci

The foci are two ordered pairs that are derived from the center and c. The c is added and subtracted from the minor axis term. If the minor axis is y, then it will be added/subtracted from that term. The foci are two ordered pairs that lie on the major axis within the ellipse. They are a key part of the graph because they indicate also whether the graph will be stretched or shrunk. They are on the major axis and the major axis tells you whether the graph will be stretched or shrunk. 

Eccentricity

 According to the SSS Packet, the eccentricity is a measure of how much the conic section deviates from being circular. To find the eccentricity of an ellipse you take c and divide it by a. This will give you a number that is less than one, but greater than zero. It is the distance from your center to your focus divided by the distance from the center to a vertex. This is shown in the image below. 

(http://freemathdictionary.com/wp-content/uploads/Eccentricity-.gif)

Major Axis

The major axis is the axis that dominates the graph. The major axis is represented by a solid line on most graphs. It contains the center, the vertices, and the foci. The major axis is seen as y=k for ellipses whose x has the larger denominator in standard form. If the y is the one who has the larger denominator then the major axis is seen as x=h. These are the lines that tell you if the graph is fat or skinny (stretched horizontally or shrunk vertically). This is an important part and will match your a, the unchanging term in your vertices, and your foci.

(http://hotmath.com/hotmath_help/topics/ellipse/ellipse-image012.gif)

Minor Axis

The minor axis is the axis that acts as a guide to size. It crosses through the center, but nothing lies on it. It has the co-vertices as endpoints. It is the b from your standard equation. It is seen as x=h if the x has the larger denominator. If the y has the larger denominator then it is y=k. This is the simple one. It is not too difficult to understand or figure out. If you look at the image above, the minor axis is pretty much an empty line. In most graphs it will be seen as a dotted line.



Vertices and Co-Vertices

The vertices and the co-vertices are probably some of the easiest points to find on a graph besides the center. The vertices are a distance from the center and the co-vertices are b distance from the center. Their constant coordinate is the one that matches what axis they lie on. If is the vertex, the constant variable will match that of the major axis and if it is the co-vertex, the constant variable will match that of the minor axis. They are your endpoints for both your major and minor axis. They are your ellipse shape guidelines.

(http://moodle.oakland.k12.mi.us/os/pluginfile.php/40772/mod_book/chapter/454/Conic_Sections/images/ellipses_ex1-3.png)

This is just another example of what an ellipse looks like on the graph. It is an example of a skinny graph because the foci have the same x and a different y, meaning that the x is the major axis.

Real World Application

An example of an ellipse in the real world is the whisper chamber in the capital building. The whisper chamber is found in statuary hall in the capital building. It is an ellipse. This room has two foci that lie in a straight line from each other on the opposite side of the room. If you stand on one of these foci and your friend on the other and you whisper something to your friend, they will be able to hear you. If you take a single step off of the focus then the sound will no longer reach your friend. This is because of he reflective properties of an ellipse. This property is an interesting one. If you drew a line in that room those two spots would be on the same line, meaning that it is the major axis. The center would be the middle ground of those two points. The reason that the whispers travel is due to the reflection off of the walls in the room. No matter what way they bounce off the wall the distance is the same. This distance is a constant. The whispers bounce off in all directions, but each one is the same.

The whispering room in the capital room is a great example of a real life ellipse because it puts into action the distance concept. The whispering spots are an equal distance from each other no matter where on the wall the sound reflects off of. This allows you to hear your friends and anyone else who might be standing on that spot at the same time that you are. It is not only found in this room though. There are other buildings in the world that do the same thing. The capital building is just a good example of where we find it in our capital. Having been in the room and testing this myself, it is very interesting to find out about. The reflection theory is present and the room is shaped like an ellipse. The foci are the gold plates on the floor and the distance is in fact the same no matter the direction of the reflection. For more information, watch the video below and read the following websites.

 





https://www.teachervision.com/math/resource/5980.html
http://www.pleacher.com/mp/mlessons/calculus/appellip.html
References
https://www.teachervision.com/math/resource/5980.html
http://www.pleacher.com/mp/mlessons/calculus/appellip.htmlhttp://moodle.oakland.k12.mi.us/os/pluginfile.php/40772/mod_book/chapter/454/Conic_Sections/images/ellipses_ex1-3.png
http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/ellipse-drawn-from-definition-geogebra-dynamic-worksheet
http://www.tpub.com/math2/Job%202_files/image777.jpg
http://www.mathwarehouse.com/ellipse/images/formul-focus.gif
http://freemathdictionary.com/wp-content/uploads/Eccentricity-.gif
http://hotmath.com/hotmath_help/topics/ellipse/ellipse-image012.gif