I/D#3: Unit Q Concept 1: Pythagorean Identities

Inquiry Activity Summary:

1. Where does sin^2x+cos^2x=1 come from?
A) First off, an identity is a proven fact or formula that is always true. The Pythagorean Theorem is an identity because it will always work, there is no number that cannot be plugged into that equation.
B) Using the letters x, y, and r we can create the Pythagorean Theorem. The Pythagorean Theorem comes from these letters. We can use x as one side, y as the other side, and r as the hypotenuse-remember the Pythagorean Theorem is for triangles- and you square all of them. Your result is the equation of x^2+y^2=r^2. These are terms we have derived from the unit circle and that is why we use them so that they can be associated with the trigonometric ratios.
C) Now we want the theorem equal to one so that we can create the identity. In order to do this we have to divide each letter by r^2. This leaves us with (x^2/r^2)+(y^2/r^2)=1. With the law of exponents we can make this a little bit easier to see and understand by making it a fraction squared for both. This leaves us with (x/r)^2+(y/r)^2=1. This is easier to understand and read.
D) Now we know that the ratio for cosine in the unit circle is (x/r). Remember that this comes from our triangles and the values they represent.
E) We also know that the ratio for sine is (y/r) which also comes from our triangles and the unit circle.
F) If you pay attention you will see that the ratios in d and e match the ratios we have in c. Using the substitution property we can replace our fractions with the functions and we have our new identity. We have cos^2(x)+sin^2(x)=1. This is what our identity is.
G) It is known as a Pythagorean Theorem Identity because all we used was the Pythagorean Theorem (which is an identity also) to figure it out and substitute some terms. It is the only formula that we used though.
H) We can verify this by using one of the angles from the unit circle. We will use a 60 degree angle. The cosine is (1/2)^2+ the sine which is (radical3/2)^2 and that produces the answer we are looking for which is one. Overall it is a working and true formula therefore it is an identity. You can also make it work with the 30 degree or 45 degree angles.

2. Show and explain how to derive the other two Pythagorean Theorem Identities from the first..
A) To get the second identity we need to divide everything in the equation by cos^2(x). This then gives us three fractions that fit with our other identities. The first is (cos^2x)/(cos^2x) which gives us the answer 1. The second is (sin^2x)/(cos^2x) which is equal to the powered up form of the reciprocal identity of tanx=sinx/cosx [Powered Up means that it is in the second or third or fourth power for each of the pieces of the identity]. That gives us tan^2x. Then the third, on the other side of the equal sign, is 1/cos^2x which is the powered up form of the reciprocal identity of secx=1/cosx. That gives us sec^2x. The resulting equation is 1+tan^2x=sec^2x. It is as easy as that.
B) To get the third one you divide the first identity by sin^2x. That gives you three fractions. The first is (cos^2x)/(sin^2x) which is the powered up form of the ratio identity of cotx=cosx/sinx. That gives us the answer cot^2x. The second fraction is sin^2x/sin^2x which is just 1. The third one on the other side of the equal sign is 1/sin^2x which is the powered up form of the reciprocal identity of cscx=1/sinx. That gives us the answer of csc^2x. The final equation-place the one in the front just to make it match the second one- is 1+cot^2x=csc^2x.

Inquiry Activity Reflection:

1) The connections that I see between Units N,O,P, and Q so far are that they are all focus on using the trigonometric ratios of sine, cosine, tangent, cosecant, secant, and cotangent. They also all are associated with the Unit Circle. Yeah for the Unit Circle!!

2) If I had to describe trigonometry in three words they would be ratios, triangles, and identities.

WPP #13/14: Unit P Concepts 6-7: Law of Sines and Cosines

This WPP13-14 was made in collaboration with Miguel G.  Please visit the other awesome posts on their blog by going here.

Into the City: A Tale Of Two Cousins

 

Problem 1: Mr. Q was on his way back from his trip to Antarctica and was flying into the Los Angeles Airport (LAX). It just so happened that his cousin Jack the Pumpkin Seller (JPS) was also flying into LAX from the small farming town in the plains. They had talked about meeting up before they got on the planes. The one thing they did not plan was where they would meet up. When Mr. Q arrived at gate 4A he got off, collected his luggage, and went to stand and look out the window. When JPS got off at gate 12A he got his luggage and went to stand by the windows. From the point where Mr. Q was standing to where JPS was standing is three hunna yards. They are both looking out at the incoming plane wondering if it is the other cousin coming in. Mr. Q is looking at it from a bearing of North 47 degrees East and JPS is looking at the same plane at a bearing of North 56 degrees West. What is the distance that Mr. Q is from the plane? What about JPS?

 

 

 

Problem 2: Mr. Q and JPS finally found each other after making a simple phone call to one another. By this time it was 4:30pm and both of the cousins were starving. Mr. Q knows of a place called Mustache Mikes right down the street and around the corner. However, JPS used his phone and thought it was down the street and around the corner in the other direction. They decided that they would go their own routes and see who was right. Mr. Q headed there at a bearing of 290 degrees while JPS headed there at a bearing of 080 degrees. Mr. Q heads in his direction at a speed of 8mph for 30 minutes and JPS heads in his direction at a speed of 6mph for 30 minutes. It turns out that Mr. Q was right. How far is JPS going to have to travel to get to the restaurant? 

 

BQ#1: Unit P: Concept 3: Law of Cosines SSS or SAS and Concept 4: Area of an oblique triangle

iii. 3. Law of Cosines - We need it because it allows us to find the missing sides and angles of oblique triangles with side angle side (SAS) or side side side (SSS). It is derived by making two right triangles, using the trigonometric ratios, and the distance formula. It is helpful and simple to understand. We derive it from a triangle in the first quadrant because all the ratios are positive and the origin is (0,0) making it all easy to derive. It works for a triangle with any lengths and with any angles. It will always work as long as the angles are realistic. The pictures below will walk you through it step by step. 

 
iv. 4. Area formulas -It is derived by drawing a line down the middle of the triangle and that creates two right triangles. Then you apply the trigonometric ratio and substitute that in for h. Now we have the area formula for an oblique triangle that looks almost the same to the one we know and love (A=.5bh), but we have our replacement for h, what h equals, and get the new formula (A=.5b(asinC)). The pictures below will walk you through it step by step. 

WPP #12: Unit O Concept 10: Angles of elevation and depression.

REMINDER! YOU HAVE TO TRY THE PROBLEMS YOURSELF AND THEN LOOK AT THE PICTURES TO CHECK! HAVE INTEGRITY!
A) Mr. Q decided that he was going to visit Antarctica. While he was down there he decided that he was going to stand on this mound of snow to look up at a group of penguins on a cliff. This meant that he was looking up at the top of the cliff from 5 feet off the ground. The base of the cliff was 180 feet away from his precious mound of snow and the cliff was 103 feet tall. What is his angle of elevation from eye level of Mr. Q? (Round to the nearest hundredth)

B) After that Mr. Q continued his adventure through the Artic. Mr. Q decided that he was going to stand up on a hill and look down at a group of penguins by the ocean of ice. His angle of depression was estimated to be about 37*. The path down the hill to the spot by the icy sea is 240 feet. How tall is the cliff that he is standing on? (Round to the nearest hundredth)

I/D2: Unit O- How can we derive the patterns for our special right triangles?

Inquiry Activity Summary
 45-45-90

Above you can see that we have an equilateral triangle. The length of each side is 1. You divide the square in a diagonal you get two triangles. Since the angles for the triangle were each 90*(because you must remember that the angles of a square add up to 360*), you now have two 90* angles and four 45* angles. Looking at the bottom triangle (the pink one) we see that each of the sides remain 1. We will label these sides a and b. The side across from the 90* angle will be the unknown c. Now that we know two of the sides we can plug it into the Pythagorean Theorem. Yeah for the Pythagorean Theorem! This is a^2+b^2=c^2. If you look at the top picture you can see it worked out completely step by step. You plug your known values in (which are 1 for both a and b) and you get c equals radical 2. That is what your diagonal is. Now this is all great if we are always working with equilaterals, but the truth is that we are not always working with them. In order to make sure that this can work with any of them, we multiply each side by the variable n. "n" just represents an unknown value. When you multiply each of the sides (a, b, and c) by n you get the new values of n (for side a), n (for side b), and n radical 2 (side c). [Clarification is on the top photo.] The variable allows a consistent expansion with any triangle that does not have the value of 1. If you look at this triangle it has the angle measurements of 45-45-90. This creates a consistent pattern for your triangles with these angle measurements. The n, n, n radical 2 will now and forever be associated with this type of triangle.

30-60-90

This is an equilateral triangle. The sum of all the angles in a triangle is 180*. Each angle has a measurement of 60*.  You divide the triangle right down the middle so that your top angle becomes two 30*, your two bottom angles remain 60*, and the split creates two 90* angles. Since an equilateral triangle is equal on all sides, your two sides on the left and right will remain 1 and your bottom side will become two sets of 1/2 because you divided it into two. Now look at the highlighted triangle and label the side across from the 90* angle c and the one across from the 60* b and finally the side across from the 30* a. If you look at the values and the variables you just put in place you see that you have two known variables and one unknown. We are going to use the Pythagorean Theorem to solve for the unknown. The theorem is a^2+b^2=c^2. You know the values for a and c. Plug those in and in the end you get b=radical 3/2. [Look at the top picture for clarification and walk through.] These all work if we were always going to use a triangle that had these measurements. However, we will not always use a 1 as the value so we need a variable and we multiply each value by the n. Wait, we also need to get rid of the fractions because we want to keep the formula consistent with every triangle we go through and fractions are not consistent so we will be multiplying all three values by 2n. If you look at the picture above you will see this worked out. Your new values are n(a 30*), n radical 3 (b 60*), and 2n (c 90*).  Now that you have these new values with the variable n you can solve other triangles that are not set with values of 1. Then if we look at other triangles with these same angle measurements we see that these form a pattern that we can depend on for 30-60-90 triangles.

 

Inquiry Activity Reflection

1. Something I never noticed before about special right triangles is that you can derive both types or triangles from a set of equilateral shapes (the triangle and the square) and also that this is how the pattern of the triangles was established. I also realized what the variable n was there for now. It was a good refresher of things I forgot and things that I never really knew.

2. Being able to derive these patterns myself aids in my learning because if I ever forget how to do it I will be able to figure it out and go back to the very beginning and work it all out. It will help me fully understand and explain how to do some of the concepts in this unit (like concepts 7 and 8) and also allows me to understand why each side is what it is. It helps me not just memorize a pattern, but really understand it and make sense of it in my head and all of the work that I do. It will forever help me.

I/D#1: Unit N Concept 7: The Unit Circle and how it relates to Special Right Triangles.

Inquiry Activity Summary

 

1) 30 Degree Right Triangle

 

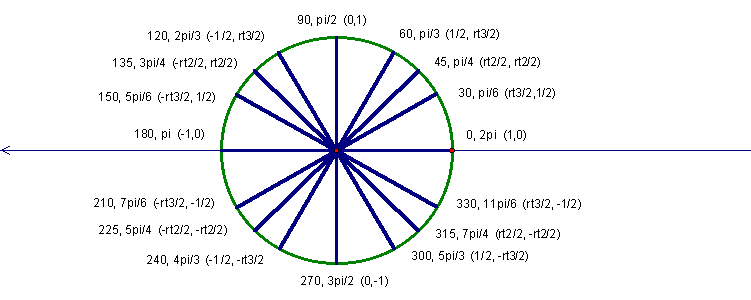
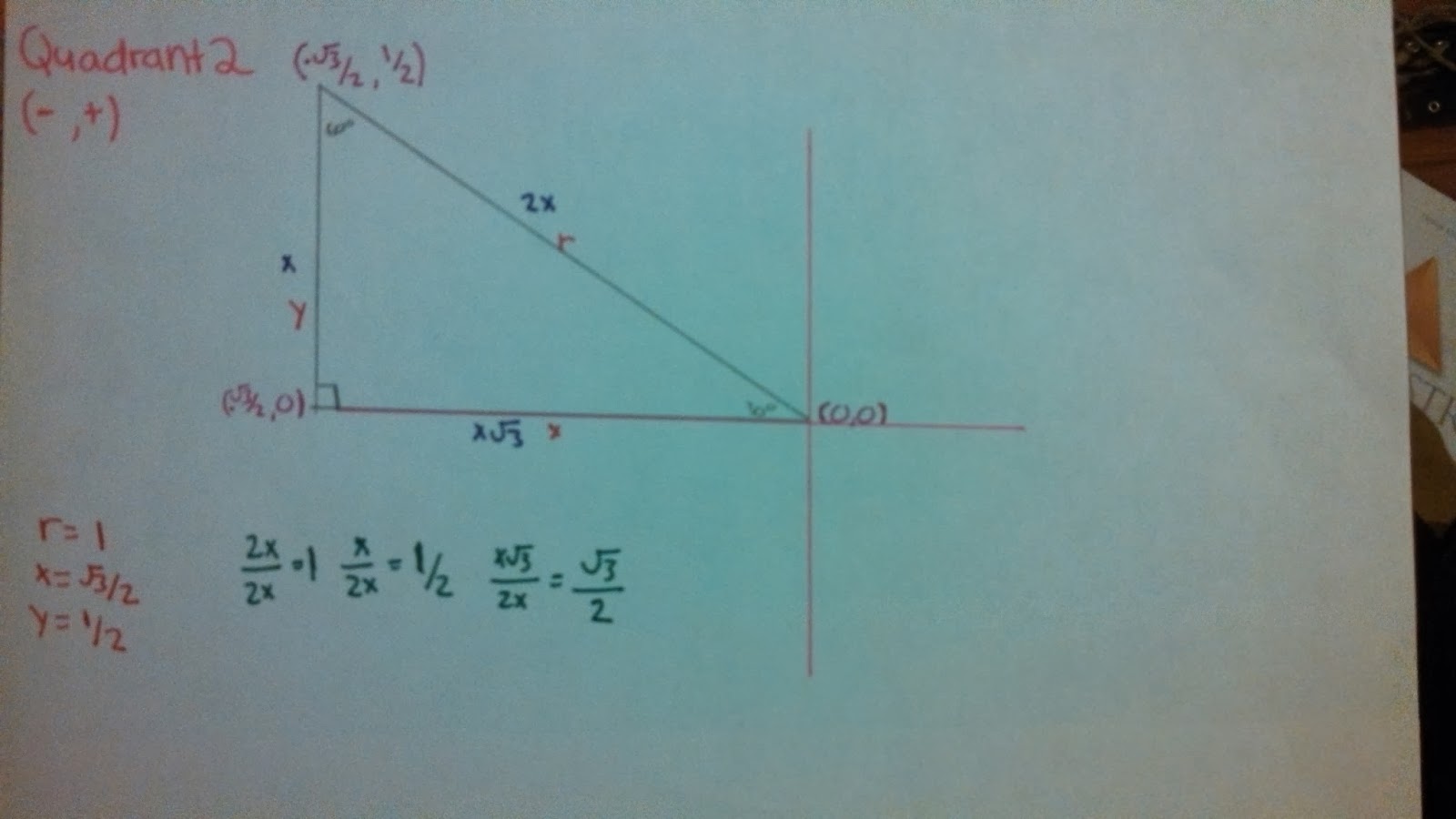
Here we have the 30 degree triangle. In the picture above we see the steps to labeling and finding the vertices of a special right triangle known as the 30-60-90 right triangle. The first thing to do is to label it according to the rules of special right triangles. This step is done in purple. It is the labeling of the vertical side, horizontal side, and the hypotenuse with the right values. The hypotenuse is labeled as 2x, the horizontal values is x radical 3, and the vertical value is simply x. The next thing that you need to do is make the hypotenuse equal to the value of one. To do this you need to divide each side by the value of the hypotenuse (2x). This step is done in green. When you divide each value by 2x your new values become 1 for the hypotenuse, radical 3 over 2 for your horizontal value, and you get 1/2 for your vertical value. After you have the new values you can label the triangle with the variables r,x, and y. When you do this you label the hypotenuse r, the horizontal side x, and the vertical value y. You then create a small chart with the new variable and the previously found value to make sure everything is clear. That step is done in red. Then you draw a graph so that the triangle is located in the first quadrant. Make the 30 degree angle the vertex with an ordered pair of (0,0). The 90 degree angle will be the horizontal value, zero-(radical 3/2, 0) and the point at the 60 degree mark as the horizontal value, vertical value- (radical 3/2, 1/2). This last value is the first mark on the unit circle.

2) 45 Degree Right Triangle

This is also a special right triangle. This one is known as the 45-45-90 triangle. The steps to solving this one are the same as the last, but the numbers are different than the last one. The first step is to label the sides according the rules of a special right triangle. The hypotenuse is to be labeled x radical 2. The vertical side is to be labeled x and so is the horizontal side. After that you want to reduce the hypotenuse to be equal to one. To do so divide every side by the value of the hypotenuse (x radical 2). The new values are shown in green. You get the hypotenuse to be 1, the vertical and horizontal sides (because they had the same value) become radical 2/2. This is done because when you divide by a radical you must rationalize it because radicals do not belong in the denominator. To do this you multiply it by radical 2 over radical 2. After that you label the sides with the variables of r,,x, and y. Label the hypotenuse r, the horizontal side x, and the vertical side y. After you do that create a small table matching the variable and the new value together. This is shown in red in the photo above. The r is equal to 1, the x any y are equal to radical 2/ 2. The next thing you do is to draw a graph so that you place the triangle in the first quadrant. Make the bottom 45 degree angle the origin with an ordered pair of (0,0). Then you move to the 90 degrees and label it as the horizontal value and zero (that is the distance that you have moved). The ordered pair is (radical 2/2, 0).  The top 45 degree angle has an ordered pair of the horizontal value and the vertical value, making it (radical 2/2, radical 2/2). That is all that is to it, This last ordered pair then becomes the second set of pairs on the unit circle. Very important to understand.

 

3) 60 Degree Right Triangle

This is our final special right triangle. It had the same values as the first special right triangle, but in different locations. It is known as the 60-30-90 right triangle. Label your hypotenuse 2x, your vertical side x radical 3 (this value always goes with the 30 degree angle) and your horizontal side as x (this value always follows the 60 degree angle. Compare this one with the 30-60-90 and see how they remain with the angle measures not sides). Then you have to make the hypotenuse equal 1 so divide each side of the triangle by 2x. When you do this you get three new values for each side. Your hypotenuse is 1, your horizontal side is 1/2, and the vertical side is now radical 3/2. This is shown in green in the picture. Then you label the sides with the variables of r,x, and y. The hypotenuse is r, the vertical side is y and the horizontal side is x. Then you match the values with the new variables. To do this create a chart with the variables and the new values. This is done in red in the picture. It is r equals 1, x equals 1/2, and y equals radical 3/2. After that is done you draw a graph so that the triangle sits in the first quadrant. Then you must label the vertices. The origin (0,0) should be at the bottom 45 degree angle. Then move down the line to the 90 degree angle and label that one x value,0 (1/2, 0). Finally go to the 30 degree angle at the top and label it the x value, y value (1/2, radical 3/2). This last ordered pair becomes your third value on the unit circle. It is very important to see this.

 

4) Derivation of the Unit Circle Assistance

(http://www.mathsisfun.com/geometry/unit-circle.html)

This activity helps you derive the unit circle because these three triangles are used for the whole circle. The top ordered pair for each triangle can be seen in each quadrant once. The values remain the same except the signs will change depending on the quadrant. From this picture though you can see how the ordered pairs keep on reappearing in the circle. The triangles make the circle a reality. The triangles in each quadrant are found the same way as the first quadrant. This works because as you move in the revolution of the circle, the larger degrees have the reference angles of the special right triangles. This is seen in the photo above. The triangles are the same in each quadrant. Below is a video that shows this happening. The person doing this is showing how no matter where you are in the circle you will have these right triangles seen. When you see that reference angle that has that 30 degrees or that 45 degrees or the 60 degrees you can follow the rules and know the ordered pair for that angle. The second video goes into details describing how the patterns are seen and where they are located in each quadrant. Both producers of the videos are showing that the right triangles are located in each quadrant just sitting in different positions.


(http://jwilson.coe.uga.edu/EMT668/EMAT6680.2001/Bruce/instructunit/day_3.htm)

(http://en.wikiversity.org/wiki/Polar_Coordinates)



 

5) Other Quadrants 

 

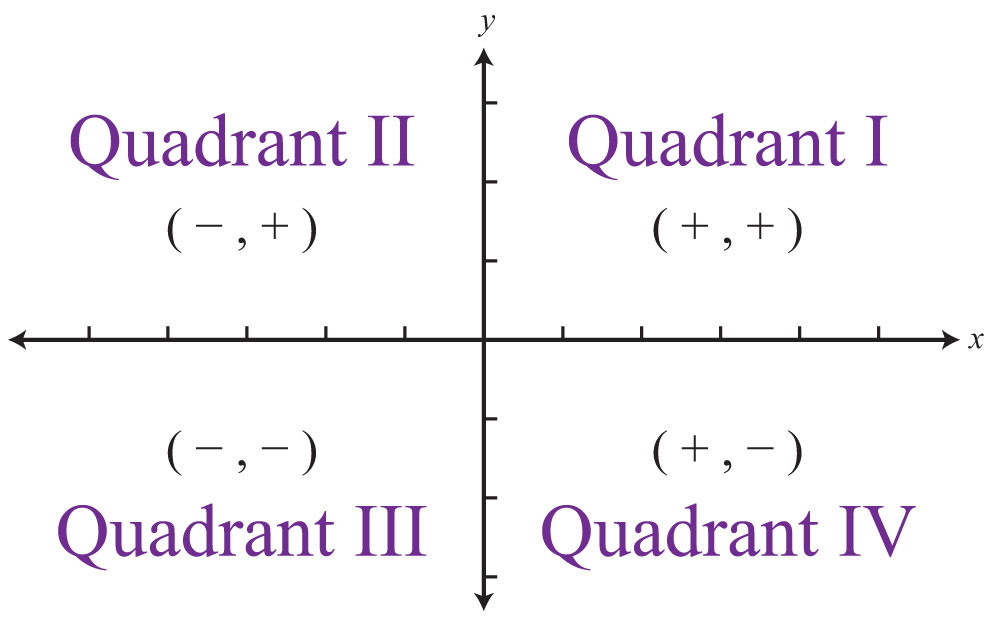
In the different quadrants the only thing about the triangles that change are that the ordered pairs will contain one or two negative values. That is due to the location of the triangle though. We know that in quadrant one they are both positive. In quadrant two the x value is negative and the y value is positive. In the third quadrant both the values are negative and in the fourth quadrant. Those are the only things that are different in the other quadrants. Nothing else changes. If you look at the images above and compare them to the quadrant one pictures you will notice that each one is identical in the process of finding it and the only thing that changes is the sign of the ordered pair. The reason that happens is it is adjusting to the different quadrant locations. Nothing else is happening to them.

(http://catalog.flatworldknowledge.com/bookhub/reader/128?e=fwk-redden-ch03_s01)

Inquiry Activity Reflection

The coolest thing I learned from this activity was that the right triangles work in all the different quadrants and that the relationship is there. I slowly realized it last year, but I was more focused on simply passing the exam last year to really appreciate it. It Is actually a very interesting thing to understand and get to use. It was very cool to learn.

This activity will help me in this unit because it will allow me to understand and easily place the ordered pairs for the triangles in the different quadrants. By doing this activity I can figure out where the triangles are in the different quadrants if I forget the pattern. This activity has allowed me to have the tools to derive the circle if I need to in a given situation.

Something I never realized before about special right triangles and the unit circle is that they were all interlocking. They work for all of the quadrants and not just the first one. I knew they worked in the first one for sure, but seeing how they worked in the other quadrants was really interesting to see. I did not fully realize that until after completing the activity. It is important to deriving the unit circle and 3 days ago I learned that. Thank you Special Right Triangles!
Resources
http://www.mathsisfun.com/geometry/unit-circle.html

http://catalog.flatworldknowledge.com/bookhub/reader/128?e=fwk-redden-ch03_s01
http://jwilson.coe.uga.edu/EMT668/EMAT6680.2001/Bruce/instructunit/day_3.htm
http://en.wikiversity.org/wiki/Polar_Coordinates



RWA#1: Unit M Concepts 4-6: Conic Sections in Real Life

1. An ellipse is the set of all points such that the sum of the distance from two points is a constant.  (http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/ellipse-drawn-from-definition-geogebra-dynamic-worksheet)
2.

(http://www.tpub.com/math2/Job%202_files/image777.jpg)



Standard Form

An ellipse has two standard forms. If you look at the image above you can see that the first one has a^2 under the x. This indicates that the graph will be a fat graph and that your major axis is equal to y and the minor axis will be equal to x. This is because the graph will have a constant y while the x changes to make the graph extend horizontally. The second equation has the a^2 under the y. This means that your graph will be skinny and that your major axis will be equal to x and your minor axis will be equal to y. This is due to the fact that your x will remain constant as you move up and down, stretching it vertically.

Center

The ellipse has a center just like every other conic. The center will always derive from the x and y binomials. If you look at the picture above, you see that x is paired with an h and y is paired with a k. Those are the numbers that you will use to write your center. The center is opposite of the numbers represented in the binomials. That means that if h is positive in the parenthesis then it will be negative in the ordered pair and vice versa. It is an easy concept to understand and you want to make sure that you do not forget to switch the signs. Remember that h will always be your x coordinate and k will always be your y coordinate.

A and B

When you look at the image above you see a^2 and b^2. These denominators will help you determine what your vertices and co-vertices will be and also help you determine your c and foci. The square root of the larger denominator will be your a. The a is the distance between your center and each of your vertices. The whole major axis is a distance of 2a. (vertex to vertex). This will allow you to figure out what your vertices are. You will move a spaces up and down or left and right depending on your graphs shape. The b is similar. You will find b by taking the square root of the smaller denominator. The b is the distance from your center to each of your co-vertices. That is either up and down or left and right from the center depending on the graphs shape. The length of the minor axis is put in terms of 2b (co-vertex to co-vertex). The b will also let you indicate what your co-vertices are by counting from the center on the minor axis that many spaces. Besides this though is the fact that they allow you to find your c.

C

The c is an important part of the graph. The c allows you to figure out your eccentricity and your foci. Your c is found by taking a^2 and subtracting b^2 to get c^2. Then you take the square root of c and simplify if possible. That answer will become your c. The c is then later used to find your foci and eccentricity.  The equation is also shown below.

 

(http://www.mathwarehouse.com/ellipse/images/formul-focus.gif)

Foci

The foci are two ordered pairs that are derived from the center and c. The c is added and subtracted from the minor axis term. If the minor axis is y, then it will be added/subtracted from that term. The foci are two ordered pairs that lie on the major axis within the ellipse. They are a key part of the graph because they indicate also whether the graph will be stretched or shrunk. They are on the major axis and the major axis tells you whether the graph will be stretched or shrunk. 

Eccentricity

 According to the SSS Packet, the eccentricity is a measure of how much the conic section deviates from being circular. To find the eccentricity of an ellipse you take c and divide it by a. This will give you a number that is less than one, but greater than zero. It is the distance from your center to your focus divided by the distance from the center to a vertex. This is shown in the image below. 

(http://freemathdictionary.com/wp-content/uploads/Eccentricity-.gif)

Major Axis

The major axis is the axis that dominates the graph. The major axis is represented by a solid line on most graphs. It contains the center, the vertices, and the foci. The major axis is seen as y=k for ellipses whose x has the larger denominator in standard form. If the y is the one who has the larger denominator then the major axis is seen as x=h. These are the lines that tell you if the graph is fat or skinny (stretched horizontally or shrunk vertically). This is an important part and will match your a, the unchanging term in your vertices, and your foci.

(http://hotmath.com/hotmath_help/topics/ellipse/ellipse-image012.gif)

Minor Axis

The minor axis is the axis that acts as a guide to size. It crosses through the center, but nothing lies on it. It has the co-vertices as endpoints. It is the b from your standard equation. It is seen as x=h if the x has the larger denominator. If the y has the larger denominator then it is y=k. This is the simple one. It is not too difficult to understand or figure out. If you look at the image above, the minor axis is pretty much an empty line. In most graphs it will be seen as a dotted line.



Vertices and Co-Vertices

The vertices and the co-vertices are probably some of the easiest points to find on a graph besides the center. The vertices are a distance from the center and the co-vertices are b distance from the center. Their constant coordinate is the one that matches what axis they lie on. If is the vertex, the constant variable will match that of the major axis and if it is the co-vertex, the constant variable will match that of the minor axis. They are your endpoints for both your major and minor axis. They are your ellipse shape guidelines.

(http://moodle.oakland.k12.mi.us/os/pluginfile.php/40772/mod_book/chapter/454/Conic_Sections/images/ellipses_ex1-3.png)

This is just another example of what an ellipse looks like on the graph. It is an example of a skinny graph because the foci have the same x and a different y, meaning that the x is the major axis.

Real World Application

An example of an ellipse in the real world is the whisper chamber in the capital building. The whisper chamber is found in statuary hall in the capital building. It is an ellipse. This room has two foci that lie in a straight line from each other on the opposite side of the room. If you stand on one of these foci and your friend on the other and you whisper something to your friend, they will be able to hear you. If you take a single step off of the focus then the sound will no longer reach your friend. This is because of he reflective properties of an ellipse. This property is an interesting one. If you drew a line in that room those two spots would be on the same line, meaning that it is the major axis. The center would be the middle ground of those two points. The reason that the whispers travel is due to the reflection off of the walls in the room. No matter what way they bounce off the wall the distance is the same. This distance is a constant. The whispers bounce off in all directions, but each one is the same.

The whispering room in the capital room is a great example of a real life ellipse because it puts into action the distance concept. The whispering spots are an equal distance from each other no matter where on the wall the sound reflects off of. This allows you to hear your friends and anyone else who might be standing on that spot at the same time that you are. It is not only found in this room though. There are other buildings in the world that do the same thing. The capital building is just a good example of where we find it in our capital. Having been in the room and testing this myself, it is very interesting to find out about. The reflection theory is present and the room is shaped like an ellipse. The foci are the gold plates on the floor and the distance is in fact the same no matter the direction of the reflection. For more information, watch the video below and read the following websites.

 





https://www.teachervision.com/math/resource/5980.html
http://www.pleacher.com/mp/mlessons/calculus/appellip.html
References
https://www.teachervision.com/math/resource/5980.html
http://www.pleacher.com/mp/mlessons/calculus/appellip.htmlhttp://moodle.oakland.k12.mi.us/os/pluginfile.php/40772/mod_book/chapter/454/Conic_Sections/images/ellipses_ex1-3.png
http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/ellipse-drawn-from-definition-geogebra-dynamic-worksheet
http://www.tpub.com/math2/Job%202_files/image777.jpg
http://www.mathwarehouse.com/ellipse/images/formul-focus.gif
http://freemathdictionary.com/wp-content/uploads/Eccentricity-.gif
http://hotmath.com/hotmath_help/topics/ellipse/ellipse-image012.gif